|
|
yureklis
Posts: 183
    
Country : Turkey | Tapa Variations Contest V
Date: 5-6 February 2011
Types: Tapa Variations
Length: 75+5 minutes
Edited by yureklis 2011-01-29 9:46 PM
|
|
yureklis
Posts: 183
    
Country : Turkey | Instruction Booklet of TVC V has been published. If you have any question, please ask under the topic. |
|
yureklis
Posts: 183
    
Country : Turkey | ATTENTION 1 PUZZLE BOOKLET WILL NOT CONTAIN EXAMPLES.
ATTENTION 2 Puzzle 8 - Double Tapa will be 85 points instead of 58, and Puzzle 9 - Tapa Connection will be 51 points instead of 39
Edited by yureklis 2011-01-30 5:57 AM
|
|
purifire

Posts: 460
      
Country : India | The Link seems to be broken! |
|
purifire

Posts: 460
      
Country : India | purifire - 2011-01-30 10:37 AM
The Link seems to be broken!
Works fine now! Thanks : ) |
|
Administrator
Country : India | |
|
rakesh_rai

Posts: 774
     
Country : India | I am having a little problem in understanding the answer key for Tapa Rotator. I am unable to understand how we get A and B for the rotated grid as shown in the IB. I am getting a different answer as shown in the attached image.
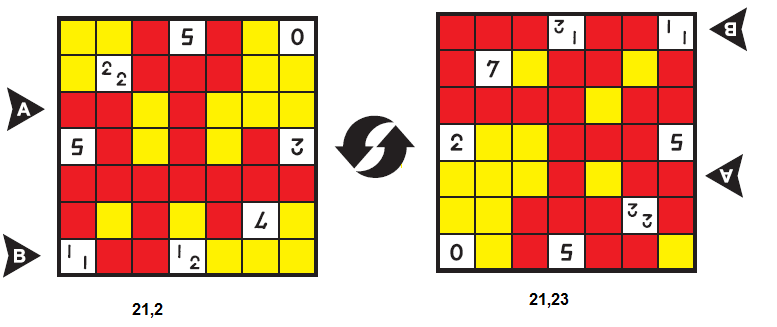 |
|
debmohanty

       
Country : India | Both grids have their own A and B.
Your marking of A and B in the rotated grid is incorrect.
May be the rows should be marked as A, B, C, D to avoid any confusion.
|
|
mucha
Posts: 13
Country : Poland | mucha posted @ 2011-02-01 2:16 PM I have a question regarding the rules of Double Tapa. Is the solution in the example unique? Why can't we add one more cell to the inside wall (the one to the right of the 4-clue) ?
Also, very nice set of variations!
Marcin |
|
yureklis
Posts: 183
    
Country : Turkey | mucha - 2011-02-01 2:16 PM
I have a question regarding the rules of Double Tapa. Is the solution in the example unique? Why can't we add one more cell to the inside wall (the one to the right of the 4-clue) ?
Also, very nice set of variations!
Marcin
Thanks for noticing, the example not have unique solution. As you noticed there is a problem with clue 4. Because there is no reason to leave the cell next to 4 empty, it may be a grey cell.
|
|
muhorka
Posts: 13
Country : Slovakia | muhorka posted @ 2011-02-01 9:55 PM I have question about Tapa Connection. "Connect the identical letters with snakelike lines going vertically or horizontally" means that lines cannot touching itself? Because line C is touching itself... |
|
yureklis
Posts: 183
    
Country : Turkey | muhorka - 2011-02-01 9:55 PM
I have question about Tapa Connection. "Connect the identical letters with snakelike lines going vertically or horizontally" means that lines cannot touching itself? Because line C is touching itself...
No, each one can touch itself. Snakelike means the line cannot have any branches. |
|
GaS
Posts: 24

Country : ITALY | GaS posted @ 2011-02-03 5:22 PM Hi all,
I have a question for Tapa Connection: all the black cells should belong to one of the snakelike lines?
Thanks,
Gabriele |
|
yureklis
Posts: 183
    
Country : Turkey | GaS - 2011-02-03 5:22 PM
Hi all,
I have a question for Tapa Connection: all the black cells should belong to one of the snakelike lines?
Thanks,
Gabriele
Yes, there cannot be a blackened cell that is not part of a line. |
|
Administrator
Country : India | Puzzle Booklet uploaded.
Notes :
the puzzle booklet has 8 pages. The first page has points distribution.the puzzle booklet does not have example grids.there are no bonus points. Ties will be sorted by last correct submission timePenalty points for submission during extra time - 12 points per minute. This applies even if your solution is incorrect |
|
Administrator
Country : India | debmohanty - 2011-01-31 11:11 AM
Both grids have their own A and B.
Your marking of A and B in the rotated grid is incorrect.
May be the rows should be marked as A, B, C, D to avoid any confusion.
In the puzzle booklet, Tapa Rotator will have marks as A & B in the top grid, and C & D in the bottom grid |
|
DreamRose311
Posts: 24

Country : United States | For Tapa w/borders, in the IB it says that clues outside the border will be invalid, but the 3 on the bottom row is. Should it be a different number, or should the instructions say 'not necessarily valid'? Thanks! looks like a lot of fun! |
|
yureklis
Posts: 183
    
Country : Turkey | DreamRose311 - 2011-02-05 4:45 AM
For Tapa w/borders, in the IB it says that clues outside the border will be invalid, but the 3 on the bottom row is. Should it be a different number, or should the instructions say 'not necessarily valid'? Thanks! looks like a lot of fun!
Yes, outside clues will be invalid, because it is needed to consider only final grid, clues are not important out of the final grid. |
|
DreamRose311
Posts: 24

Country : United States | Is it just me or is the file not working? Has anyone else tried to start yet? |
|
brianklimek
Posts: 14
Country : United States | HELP!! Ive started the contest and timer, and the puzzle booklet is "not available"??? |
|
brianklimek
Posts: 14
Country : United States | Im getting the following message:
Server Error404 - File or directory not found.
The resource you are looking for might have been removed, had its name changed, or is temporarily unavailable.
What do I do? |
|
brianklimek
Posts: 14
Country : United States | You still online trying to get this to work? |
|
brianklimek
Posts: 14
Country : United States | Hello - I started the contest and cannot get the puzzle booklet. Is it possible to reset me, UserID is brianklimek, and I will try again tomorrow night? I really would like to take part in this TAPA contest.
Thanks.
Brian Klimek |
|
debmohanty

       
Country : India | brianklimek - 2011-02-05 10:03 AM
Hello - I started the contest and cannot get the puzzle booklet. Is it possible to reset me, UserID is brianklimek, and I will try again tomorrow night? I really would like to take part in this TAPA contest.
Thanks.
Brian Klimek
Hi Brian, There was typo in the download link. It is fixed now. You should be able to download the file - Here is the download link - http://logicmastersindia.com/lmitests/dl.asp?attachmentid=107
Also, your start record has been deleted, you can Start the contest again.
Please post here if you face any problems.
|
|
debmohanty

       
Country : India | DreamRose311 - 2011-02-05 8:24 AM
Is it just me or is the file not working? Has anyone else tried to start yet?
There was a typo in the link. It is fixed now. |
|
yureklis
Posts: 183
    
Country : Turkey | ATTENTION
Word Tapa: There is an unclear phrase in the instructions. Each word should intersect or overlap with another one, but the instruction doesn't state this clearly. E.g. if there are two words as ONE and TWO, they can be TWONE but they cannot be TWOONE or ONETWO.
All submissions will be checked manually. You can solve the puzzle as you like, the solutions will be accepted if it is correct with or without intersecting every word.
Edited by yureklis 2011-02-05 9:48 PM
|
|
rakesh_rai

Posts: 774
     
Country : India | Nice puzzles - neither too easy nor too difficult. Although I was not able to attempt a majority of the puzzles, I enjoyed the ones which I could. Thanks Serkan for the nice contest. |
|
StGeorge
Posts: 11
Country : Bulgaria | Great puzzles, I still haven't finished all of them, but I'll be sure to do so.
I realised, though, that I have posted my answers to the Tapa with Borders puzzles in the fields for the Tapa Possible puzzles. It would be very much appreciated if you could amend this error on my part.
I guess the error-checking system isn't of much use when the answers to all puzzles have the same format :) |
|
yureklis
Posts: 183
    
Country : Turkey | StGeorge - 2011-02-06 3:00 AM
Great puzzles, I still haven't finished all of them, but I'll be sure to do so.
I realised, though, that I have posted my answers to the Tapa with Borders puzzles in the fields for the Tapa Possible puzzles. It would be very much appreciated if you could amend this error on my part.
I guess the error-checking system isn't of much use when the answers to all puzzles have the same format :)
: ) I sent a message you about it. And i asked this. Of course you get points. But i think there are some technical issues in this situation, so probably administrator can fix this. |
|
forcolin

Posts: 172
   
Country : ITALY | I believe there is another bad sentence on the WORD TAPA puzzle.
"Different words can intersect only if they share a letter" says the booklet. but in the example VARIATION and CONTEST share TWO letters (ON).
should the instruction say "if they share at least a letter"? |
|
MellowMelon

Country : United States | Question on Tapa Star from someone who has done the test: does the count of cells between the two stars include the two stars themselves? I interpreted as if the stars in a row were in column 1 and column 6, then 4 would be entered for that row (columns 2,3,4,5 are between them). If that's not what you meant, can credit still be given? |
|
debmohanty

       
Country : India | MellowMelon - 2011-02-06 6:30 AM
Question on Tapa Star from someone who has done the test: does the count of cells between the two stars include the two stars themselves? I interpreted as if the stars in a row were in column 1 and column 6, then 4 would be entered for that row (columns 2,3,4,5 are between them). If that's not what you meant, can credit still be given?
You already have points for Tapa Star - You can check your submissions and points here http://logicmastersindia.com/TVC/V/score.asp |
|
brianklimek
Posts: 14
Country : United States | Thanks Deb. |
|
motris
Posts: 199
    
Country : United States | motris posted @ 2011-02-06 11:51 AM Beautiful test Serkan. I eagerly await the next one! |
|
harmeet
Posts: 87
   
Country : India | harmeet posted @ 2011-02-06 2:28 PM serkan,
very nice set of puzzles.
for tapa rotator i combined row A and row B answers in the first row and second rotator puzzle's answer in the next row, amounting to both puzzles tagged as incorrect. can this be considered?
thanks and regards,
Harmeet |
|
Administrator
Country : India | harmeet - 2011-02-06 2:28 PM
for tapa rotator i combined row A and row B answers in the first row and second rotator puzzle's answer in the next row, amounting to both puzzles tagged as incorrect. can this be considered?
done. |
|
zhergan
Posts: 32

Country : Turkey | zhergan posted @ 2011-02-06 9:26 PM  Serkan for really nice set of puzzles  and LMI for hosting
this event. Tapa is a really nice puzzle type and its different
variants increased a lot. Just by looking at normal tapa and its
many variants I hope you will invent some other new puzzle types
in the future...
Regards,
Zafer |
|
tamz29
Posts: 225
  
Country : Thailand | tamz29 posted @ 2011-02-07 12:16 AM Awesome puzzles!
I got penalised on time, but manage to get all my solutions correct.
I need to practise some more tapas... |
|
David McNeill
Posts: 63
  
Country : United Kingdom | I'm afraid I found this contest just too difficult. Obviously a lot of practice needed. The puzzles which I finished in the time were all very nicely designed and I look forward to trying the others later.
David McNeill. |
|
yureklis
Posts: 183
    
Country : Turkey | David McNeill - 2011-02-07 3:28 AM
I'm afraid I found this contest just too difficult. Obviously a lot of practice needed. The puzzles which I finished in the time were all very nicely designed and I look forward to trying the others later.
David McNeill.
I agree with you. I didnt make puzzles in different difficulties, i have a reason for this. In the last year we didnt use any bonus points, and in this year we dont want to break TVC rules. I had to make most of puzzles not easy due to lack of bonus points. Because we dont want to have a lot of participants who solved all puzzles. But i am afraid of not being good. So we decided to make much more puzzles than TVC V so that offering much more easy puzzles to all participants in next contests. We think that is better.
Best,
Serkan Edited by yureklis 2011-02-07 3:47 AM
|
|
forcolin

Posts: 172
   
Country : ITALY |
Serkan
good set of puzzles as usual. a bit confused about tapa word do not understand why the second puzzle is wrong, perhaps did not understand the rule about overlapping of words.
Pity because costed me penalty points to amend a typo from the solution which was wrong anyway
stefano |
|
yureklis
Posts: 183
    
Country : Turkey | forcolin - 2011-02-07 4:00 AM
Serkan
good set of puzzles as usual. a bit confused about tapa word do not understand why the second puzzle is wrong, perhaps did not understand the rule about overlapping of words.
Pity because costed me penalty points to amend a typo from the solution which was wrong anyway
stefano
Stefano, you got the points from second word tapa. In the forum we announced that we check manually word puzzles solutions because of some ambiguous instruction . So your solution is correct, and you got the points. |
|
yureklis
Posts: 183
    
Country : Turkey | First contest of 2011 Tapa Series is over, many thanks to all participants and LMI.
The top three competitors are:
1- Thomas Snyder (USA ) - 15/15 - 49:01
2- Andrey Bogdanov (Russia ) - 15/15 - 71:27
3- Florian Kirch (Germany ) - 15/15 - 72:32
Results can be viewed: http://logicmastersindia.com/TVC/V/score.asp
Congratulations to Thomas for first victory of Tapa 2011 Series. He solved all puzzles in amazing total times. I think in this year Tapa Series will be more challening for everyone.
* TVC V has 15 puzzles, and next contests will have much more puzzles than this.
*
- The puzzle solved by least competitors was 10B - Tapa Possible.
- The puzzle solved by most competitors was 2 - Tapa Filler.
- The puzzle with the highest rating was 10B - Tapa Possible and the puzzle with the lowest rating was 2- Tapa Filler.
* Last year we mostly prefered to get B/W answering format. All competitors had to enter marked row/column contents. But this was hard for all of us, so we changed the general answer format. This one is shorter and easier than the old one. But as a contest designer I have doubts in this answer format, about the puzzles being solved almost completely by competitors. So I chose some rows which need being more careful, like Tapa Filler second row, or 2nd Tapa rotator first row. Please remember this for next contests.
* We will follow same pattern like previous year. So, your first contest results will be transferred to the general table multiplied by a constant. I think the table will be available after TVC VI.
* Same like last year contests' total points will rise, of course penalty points too.
* Please remember in this year best 3 results out of 4 will be considered. So, it is not important to have one bad performance.
* TVC VI instruction will be published on 14 February.
* One more thing, if you have variation ideas please share us.
All the best,
Serkan Yurekli Edited by yureklis 2011-02-07 7:52 AM
|
|
debmohanty

       
Country : India | Congratulations to Thomas for winning this contest (and also for winning Sudoku Cup V).
|
|
debmohanty

       
Country : India | Thomas took just 49 minutes, and after that we checked to find that we've his split submission timings information stored in the database. I thought it will be interesting to share it here.
| SubmitTime | PuzzleName | | 0:04:02 | 2 - Tapa Filler | | 0:08:05 | 1 - Tapa Chess | | 0:11:11 | 3 - Math Tapa | | 0:22:59 | 5C - Word Tapa | | 0:22:59 | 5B - Word Tapa | | 0:22:59 | 5A - Word Tapa | | 0:26:10 | 4 - Tapa Star | | 0:29:25 | 6B - Tapa Rotator |
| 0:29:25 | 6T - Tapa Rotator | | 0:32:50 | 7A - Tapa with Borders | | 0:35:06 | 7B - Tapa with Borders | | 0:38:50 | 8 - Double Tapa | | 0:41:54 | 9 - Tapa Connection | | 0:44:23 | 10A - Tapa Possible | | 0:49:01 | 10B - Tapa Possible |
I had an email exchange with him and here is what he had to say regarding his timings.
>>
So what I do on a test is submit puzzles when I finish a sheet and discard it to the floor. Sometimes I'll do this independently when there are two puzzles on a side, but certainly a full side when that's done as after I check the entry I won't look back at that page until everything is done.
You can see I solved from front to back (generally ). I made a mistake in putting stars into the Tapa Star the first time through (there is a single cell that the Tapa can grow into that is necessary to solve it and I didn't consider this the first time ), so I printed a new grid to put the wall in and restart the labeling. During this time I jumped and did the Words. So the gap to finish Tapa Star is not perfectly accurate. More like 3 minutes just to put the stars on it from the time data you see. Rotator was straightforward. Borders involved being lucky with 6x6 blocks a little bit (I excluded two edges in each case ). Double Tapa was easy for me as I had learned the 221 corner break-in from some Crocopuzzle practice, and then I saw how to go along the right edge with the other wall. It was a very fun puzzle. Tapa Connection involved a few trials around the A and D, but eventually once I got one good path I could get the rest quickly. The Tapa Possible were really fun and at least the second solved from considering how the white clue areas would block you from getting to some of the grays twice. Figuring out to leave corners blank for the 3/3 gave a good nucleation site for the rest to grow out. Tapa is a puzzle type where some logic and also some intuition from a guess can work together really well. I got lucky more often than not this time around. We'll see how TVC VI goes.
>>
|
|
AndreyBogdanov
Posts: 44
 
Country : Russia | Thanks a lot for a beautiful contest. I had a lot of fun during solving.
Looking forward for the next parts. |
|
Nikola
Posts: 103

Country : Serbia | Nikola posted @ 2011-02-07 2:09 PM Good start of the new season of tapa. Congrats to Thomas for an excellent time and also congrats to other toppers!
I didn't forget to submit my last puzzle. Somehow, but I still don't know how, I imagined in double tapa that two tapas cannot form 2x2 square. After the competition, when I realized where I'm wrong, I solved the puzzle in two minutes. Very stupid mistake. 
Serkan, thanks for the password! 
Nikola |
|
forcolin

Posts: 172
   
Country : ITALY | debmohanty - 2011-02-07 9:23 AM
Thomas says
>>
So what I do on a test is submit puzzles when I finish a sheet and discard it to the floor. >>
Next time, could I play while sitting on the floor of Thomas' room?   |
|
Valezius
Posts: 66
  
Country : Hungary | Thank you Serkan, this was a really good competition.
The TAPA STAR and TAPAPOSSIBLE are very good new tapa variations. However, the WORD TAPA won't be my favourite tapa variation :) |
 TVC V
TVC V TVC V
TVC V