


Country : India
Administrator posted @ 2010-10-11 8:32 AM
 @ 2010-10-11 8:32 AM (#2133 - in reply to #2132) (#2133) Top
@ 2010-10-11 8:32 AM (#2133 - in reply to #2132) (#2133) Top



Country : India
Administrator posted @ 2010-10-11 8:32 AM
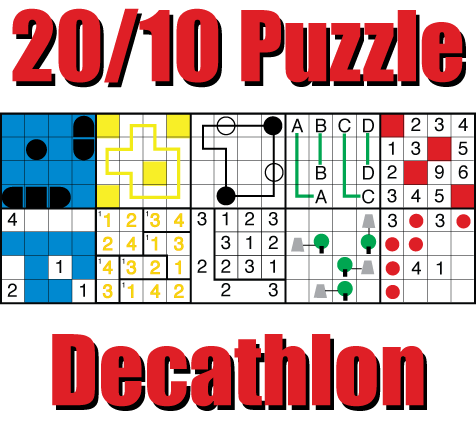
Author : Thomas Snyder
Date : 16th and 17th October
Puzzle Types : 10 Selected puzzle types - an Easy, a Hard and a Mutant from each type
Length : 120 minutes
IB and Submission Link : http://logicmastersindia.com/M201010P2
 @ 2010-10-11 10:42 AM (#2134 - in reply to #2133) (#2134) Top
@ 2010-10-11 10:42 AM (#2134 - in reply to #2133) (#2134) TopPosts: 774






Country : India
rakesh_rai posted @ 2010-10-11 10:42 AM
 @ 2010-10-11 11:03 AM (#2135 - in reply to #2132) (#2135) Top
@ 2010-10-11 11:03 AM (#2135 - in reply to #2132) (#2135) TopPosts: 774






Country : India
rakesh_rai posted @ 2010-10-11 11:03 AM
 @ 2010-10-11 12:43 PM (#2138 - in reply to #2132) (#2138) Top
@ 2010-10-11 12:43 PM (#2138 - in reply to #2132) (#2138) TopPosts: 199





Country : United States
motris posted @ 2010-10-11 12:43 PM
Thanks for catching these errors (we've been very mindful to check the puzzles out, but I didn't double check the IB figures and you've found two obvious mistakes).
On the first battleships example, the sub in R6C4 should be in R4C4, and the answer entry for the first part is 000001.
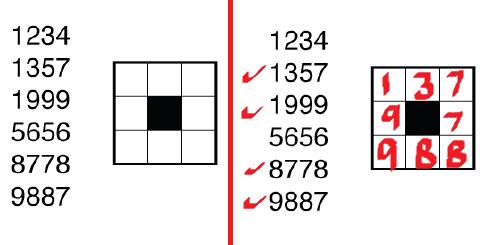
On the second number skeleton, you have found another valid solution as the example is under-constrained. Change the 8778 to 8877.
Edited by motris 2010-10-11 12:46 PM
 @ 2010-10-11 1:13 PM (#2139 - in reply to #2132) (#2139) Top
@ 2010-10-11 1:13 PM (#2139 - in reply to #2132) (#2139) Top








Country : India
debmohanty posted @ 2010-10-11 1:13 PM
While top solvers will target to get all 450 bonus points, others have to think of strategy to maximize their points including the bonus.
Given that I can't finish all 30 in 2 hours, I would probably finish all easy ones (securing 150 bonus) and then solve both hard and mutant ones I'm more comfortable with (read : favorite).
I like that fact that full 150 points will be given even if 9 were correct. That is a nice consideration.
 @ 2010-10-11 1:17 PM (#2140 - in reply to #2132) (#2140) Top
@ 2010-10-11 1:17 PM (#2140 - in reply to #2132) (#2140) Top








Country : India
debmohanty posted @ 2010-10-11 1:17 PM
While the example is too small to reveal much, I invite others to create bigger size puzzles and share here.
 @ 2010-10-11 3:50 PM (#2143 - in reply to #2140) (#2143) Top
@ 2010-10-11 3:50 PM (#2143 - in reply to #2140) (#2143) TopPosts: 349





Country : India
amitsowani posted @ 2010-10-11 3:50 PM
 @ 2010-10-11 5:49 PM (#2147 - in reply to #2132) (#2147) Top
@ 2010-10-11 5:49 PM (#2147 - in reply to #2132) (#2147) TopPosts: 40


Country : China
Minfang Lin posted @ 2010-10-11 5:49 PM
And i changed battleships and number skeleton pictures there.
 @ 2010-10-11 5:58 PM (#2148 - in reply to #2143) (#2148) Top
@ 2010-10-11 5:58 PM (#2148 - in reply to #2143) (#2148) Top








Country : India
debmohanty posted @ 2010-10-11 5:58 PM
In Calcudoku is it necessary for subtraction and division to only apply to regions with two numbers?
But it is probably best to have Thomas say the final word on this.
 @ 2010-10-11 8:41 PM (#2151 - in reply to #2132) (#2151) Top
@ 2010-10-11 8:41 PM (#2151 - in reply to #2132) (#2151) TopPosts: 199





Country : United States
motris posted @ 2010-10-11 8:41 PM
For the Total Masyu mutant, I have some earlier examples that did not use the gray circle gimmick here. You can at least learn some of the ideas from those puzzles. The competition puzzle, like the example, however uses only gray circles so knowing what are white and black circles will be an extra part of that puzzle.
Edited by motris 2010-10-11 8:43 PM
 @ 2010-10-11 11:01 PM (#2155 - in reply to #2132) (#2155) Top
@ 2010-10-11 11:01 PM (#2155 - in reply to #2132) (#2155) TopPosts: 24

Country : United States
DreamRose311 posted @ 2010-10-11 11:01 PM
Very much looking forward to the test. Looks like a lot of fun, and the bonus system is a really cool idea... Definitely have a lot of thoughts in my head on how I should strategize solving order...
Also, Thanks so much to LMI for having lots of puzzle competitions!! It is soooo much better than having to wait for yearly puzzle/sudoku championships to roll around.
 @ 2010-10-12 12:03 AM (#2157 - in reply to #2132) (#2157) Top
@ 2010-10-12 12:03 AM (#2157 - in reply to #2132) (#2157) TopPosts: 11
Country : Bulgaria
StGeorge posted @ 2010-10-12 12:03 AM
Thomas, I am curious as to how many points you think the winner will have earned. Assuming that it's unlikely that someone solves everything.
 @ 2010-10-12 1:00 AM (#2158 - in reply to #2155) (#2158) Top
@ 2010-10-12 1:00 AM (#2158 - in reply to #2155) (#2158) TopPosts: 199





Country : United States
motris posted @ 2010-10-12 1:00 AM
There is a 3x10 grid on the title page that may help you track progress.
 @ 2010-10-12 1:13 AM (#2159 - in reply to #2157) (#2159) Top
@ 2010-10-12 1:13 AM (#2159 - in reply to #2157) (#2159) TopPosts: 199





Country : United States
motris posted @ 2010-10-12 1:13 AM
I am very much looking forward to this - I'm sure the puzzles will be top-notch and some of the mutants seem really intriguing. Also, the bonus system looks like a lot of fun, it would definitely encourage solvers to try out puzzle types that they would have otherwise avoided during the time limit.
Thomas, I am curious as to how many points you think the winner will have earned. Assuming that it's unlikely that someone solves everything.
The test was written with the range of LMI solvers in mind (everyone from world champion uvo to new competitors who may have never done a competition or who may be most familiar with sudoku). I expect that there will be a few solvers that can finish everything, in accord with our play-test results, but that the majority of solvers will be in a situation where they are picking which puzzles in a type to solve either to finish out an intermediate bonus. Starting with the harder examples will be worth more points in general, and then as time runs short solvers can turn to "easy" reliably to finish out a group, or people can start by clearing everything at "easy" and then choosing between "hard" or "mutant" for the second. Knowing strengths/weaknesses and budgeting time accordingly will be important for most since finishing the test will not be possible for everyone.
The bonus system was inspired by WPC Brazil which tried to achieve a similar goal (diverse solving) but in what I felt was a less effective way. Basically, each round there was split into 3/4 sections and the first puzzle solved in a section was worth more than the second which was worth more than the third and so on. The problem was that the first puzzle was often worth 30 points, the fourth puzzle worth 3 points, and score bunching happened so the overall scores were dominated by rounds where solvers earned placement/time bonuses, often worth 100x the amount of the "last puzzle" solved. Instead of being logarithmic in score, here there are exponential increases in score based on completing some number of goals. It also gives good goals for solvers at all levels. Earning even the first 150 point bonus is a great achievement for many solvers, and is something to aim for by trying some new styles instead of just doing, say, the Battleships.
 @ 2010-10-12 2:53 AM (#2160 - in reply to #2132) (#2160) Top
@ 2010-10-12 2:53 AM (#2160 - in reply to #2132) (#2160) TopPosts: 1
Country : United States
jrivet posted @ 2010-10-12 2:53 AM
 @ 2010-10-12 3:29 AM (#2161 - in reply to #2160) (#2161) Top
@ 2010-10-12 3:29 AM (#2161 - in reply to #2160) (#2161) TopPosts: 199





Country : United States
motris posted @ 2010-10-12 3:29 AM
According to the example for Big Tent Party, the numbers outside the grid are the number of cells covered by tents, not the number of tents as stated in the rules.
Your observation is correct, and the abbreviated instructions for the variation have not corrected for the difference. All cases should be read as "number of cells covered by tents" which happens to equal the number of tents in the normal form but does not in the mutant. The example images for both types use numbers in the intended way, as does the answer entry.
 @ 2010-10-12 1:17 PM (#2167 - in reply to #2132) (#2167) Top
@ 2010-10-12 1:17 PM (#2167 - in reply to #2132) (#2167) TopPosts: 460







Country : India
purifire posted @ 2010-10-12 1:17 PM
Rishi
 @ 2010-10-12 5:59 PM (#2169 - in reply to #2167) (#2169) Top
@ 2010-10-12 5:59 PM (#2169 - in reply to #2167) (#2169) TopPosts: 349





Country : India
amitsowani posted @ 2010-10-12 5:59 PM
Rule says : All cells need not be visited.
and the answer key says : Starting from "A"..........
Can we assume that the cell with "A" in it will definitely be visited?
 @ 2010-10-12 8:06 PM (#2170 - in reply to #2167) (#2170) Top
@ 2010-10-12 8:06 PM (#2170 - in reply to #2167) (#2170) TopPosts: 152



Country : United Kingdom
detuned posted @ 2010-10-12 8:06 PM
though Im not a great fan( read solver) of puzzles, this is one test I am definitely going to attempt .... not everyday we get a chance to attempt puzzles by Thomas
Rishi
Perhaps not every day, but certainly every week :)
I must say I'm looking forward to this one and have no doubts at all this will make up for the failings of the last test! Especially the Numberlink. Although I'm a little disappointed to see that 0 is definitely out of the set for the mutant "TomTom" ;)
 @ 2010-10-12 9:04 PM (#2171 - in reply to #2169) (#2171) Top
@ 2010-10-12 9:04 PM (#2171 - in reply to #2169) (#2171) TopPosts: 199





Country : United States
motris posted @ 2010-10-12 9:04 PM
In Simple Loop Mutant :
Rule says : All cells need not be visited.
and the answer key says : Starting from "A"..........
Can we assume that the cell with "A" in it will definitely be visited?
This is a safe assumption, but you'll realize when you see the puzzle that knowing A is visited is not really a benefit over a version of the puzzle with no letters inside.
 @ 2010-10-12 9:23 PM (#2172 - in reply to #2132) (#2172) Top
@ 2010-10-12 9:23 PM (#2172 - in reply to #2132) (#2172) TopPosts: 11
Country : Bulgaria
StGeorge posted @ 2010-10-12 9:23 PM
Quote from the IB: Each shape represents exactly one white area in the grid and each white area is represented by exactly one shape outside the grid"
Does this mean that there will be no more than 1 "1" / 1 "2" / 2 "3"s / 5 "4"s / etc in the puzzle, due to the limited number of possible n-ominoes?
 @ 2010-10-12 9:33 PM (#2173 - in reply to #2172) (#2173) Top
@ 2010-10-12 9:33 PM (#2173 - in reply to #2172) (#2173) TopPosts: 199





Country : United States
motris posted @ 2010-10-12 9:33 PM
Here's a question about the mutant nurikabe.
Quote from the IB: Each shape represents exactly one white area in the grid and each white area is represented by exactly one shape outside the grid"
Does this mean that there will be no more than 1 "1" / 1 "2" / 2 "3"s / 5 "4"s / etc in the puzzle, due to the limited number of possible n-ominoes?
There will be no repeated shapes outside the grid in this puzzle, so your "limits" are correct for what you might expect. Note that just like the example each island still maintains its correct number so if there is just 1 "3" island outside, say the bent one, then you know the 3 in the grid must adopt the bent shape and not the linear shape, which would not be the case in the regular puzzle.
 @ 2010-10-14 4:56 AM (#2184 - in reply to #2140) (#2184) Top
@ 2010-10-14 4:56 AM (#2184 - in reply to #2140) (#2184) TopPosts: 30

Country : Canada
figonometry posted @ 2010-10-14 4:56 AM
About the Mutants : While most of the mutants look interesting, the Masyu mutant look best to me.
While the example is too small to reveal much, I invite others to create bigger size puzzles and share here
How about this? (Answer is here: Figonometry)
 @ 2010-10-14 6:58 AM (#2186 - in reply to #2184) (#2186) Top
@ 2010-10-14 6:58 AM (#2186 - in reply to #2184) (#2186) Top








Country : India
debmohanty posted @ 2010-10-14 6:58 AM